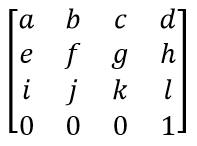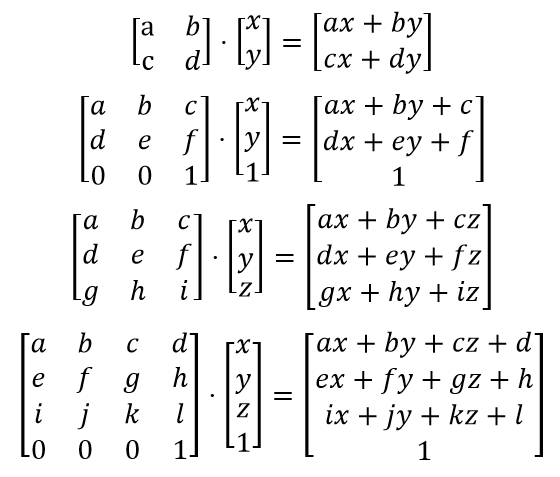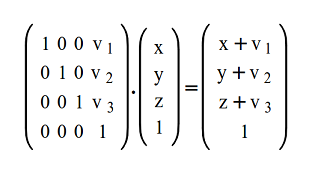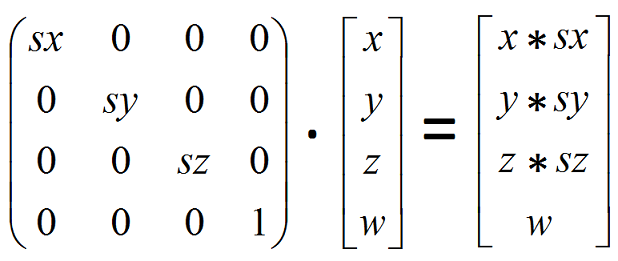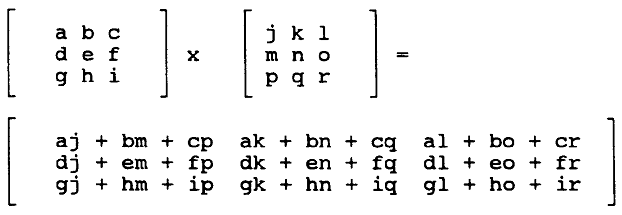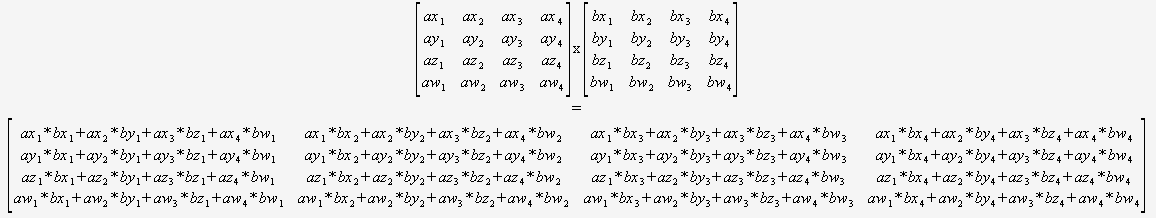-
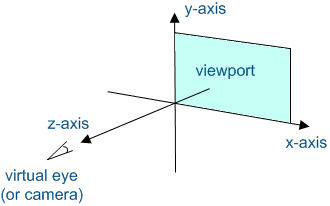
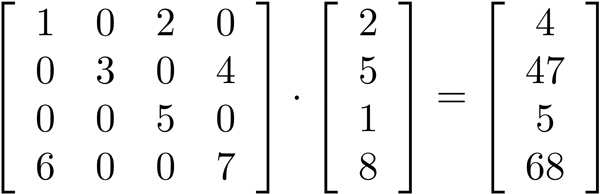
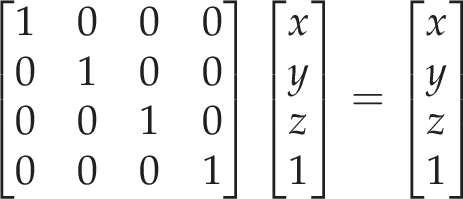
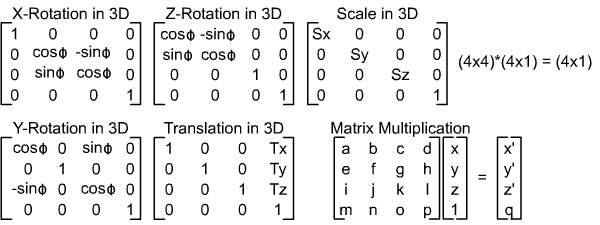
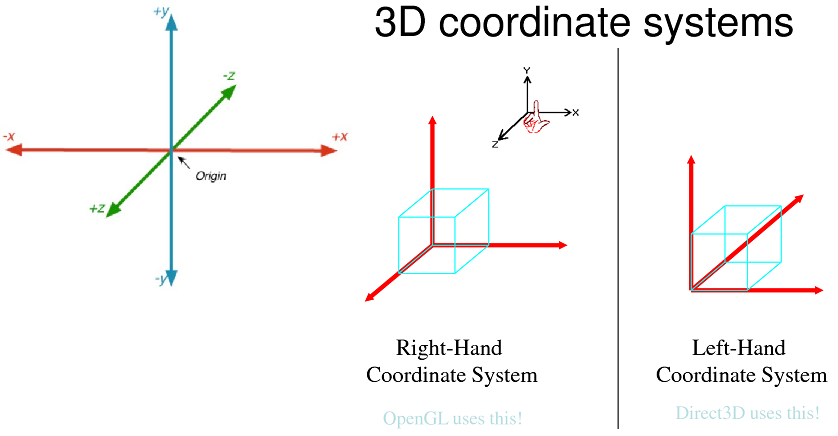
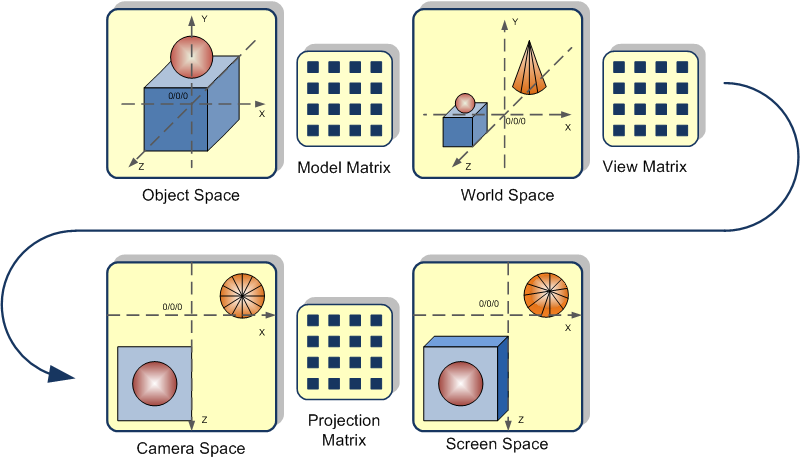
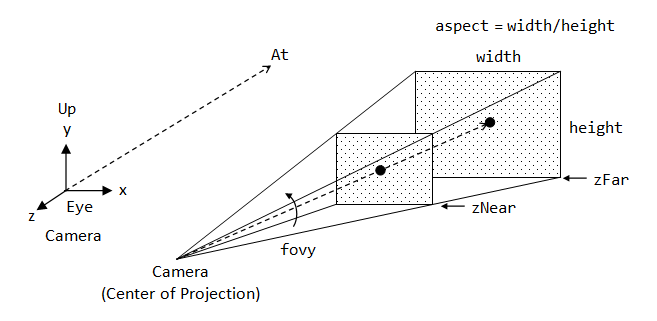
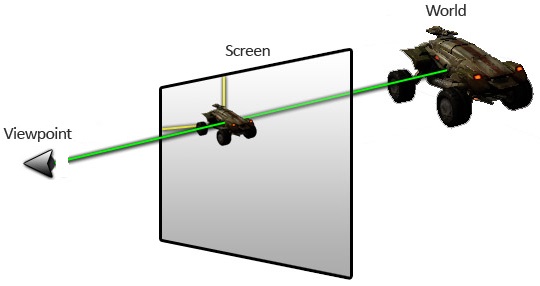
Cartesian coordinates are typically used to represent the world in 3D programming.
-
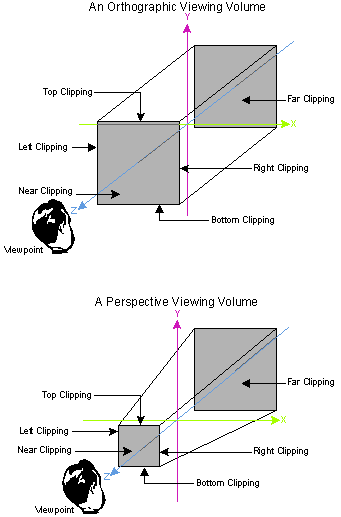
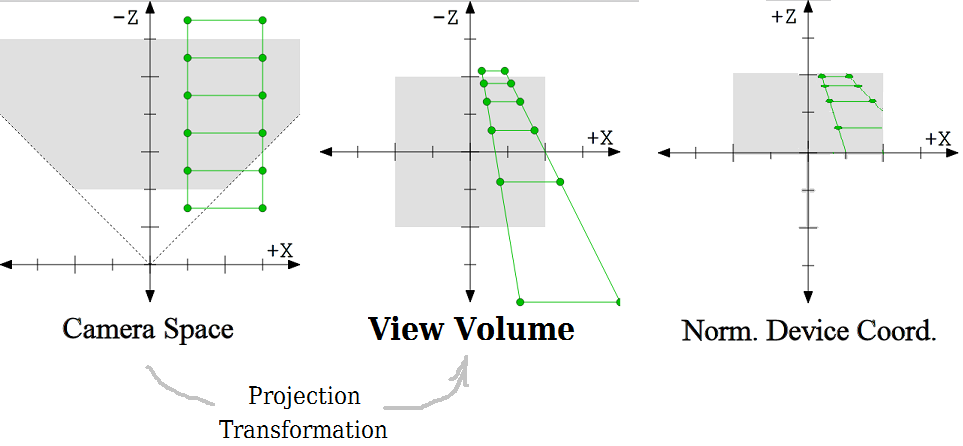
When creating a window, we must define where is our viewport in the Cartesian system
-
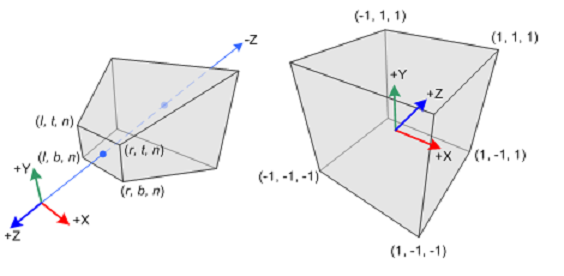
Middle of screen is (0, 0)
-
Dimensions are as follows:
-
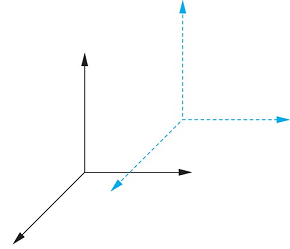
x = horizontal
-
y = vertical
-
z = depth (can be RHS or LHS)
-
(0, 0, 0) is origin
-