Java Programming I on YouTube:
https://www.youtube.com/playlist?list=PLLIqcoGpl73iaXAtS_-V_Xdx3mhTzPwb5
--------------------------------------------------------------- Type Bytes Usage ------ ----- ---------------------------------------------- byte 1 Very short integers from -128 to 127 --------------------------------------------------------------- short 2 Short integers from -32,768 to 32,767 --------------------------------------------------------------- int 4 Integers from -2,147,483,648 to 2,147,483,647 --------------------------------------------------------------- long 8 Long integers from -9,223,372,036,854,775,808 to 9,223,372,036,854,775,807 --------------------------------------------------------------- float 4 Single-precision, floating-point numbers from -3.4E38 to 3.4E38 with up to 7 significant digits --------------------------------------------------------------- double 8 Double-precision, floating-point numbers from -1.7E308 to 1.7E308 with up to 16 significant digits --------------------------------------------------------------- char 2 A single Unicode character stored in two bytes --------------------------------------------------------------- boolean 1 A true or false value ---------------------------------------------------------------
To express the value of a floating-point number, you can use scientific notation like 2.382E+5, which means 2.382 times 105 (a value of 238,200), or 3.25E-8, which means 3.25 times 10-8 (a value of .0000000325). Java will sometimes use this notation to display the value of a float or double data type.
Because of the way floating-point numbers are stored internally, they can't represent the exact value of the decimal places in some numbers. This can cause a rounding problem in some business applications.
You should be careful when comparing floating-point numbers for equality:
One way to check whether two floating-point numbers are equal is to check whether the absolute value of their difference is less than a certain tolerance.
For example, suppose the tolerance is .000001.
Then double x and y are equal if the absolute value of difference
(x – y)
is less than 0.000001.
To find the absolute value, you can use the function Math.abs of the Math class:
Math.abs(x – y) < 0.000001
The above expression determines whether the absolute value of (x – y) is less than 0.000001.
Scientific notation (exponential notation) adjusts specified decimal point to the left or to the right according to the specified value of exponent e.
The e-suffix represents times ten raised to the power. For example,
1e-2 == 0.01 == 1×10-2
1e-1 == 0.10 == 1×10-1
1e-0 == 1.00 == 1×100
1e+0 == 1.00 == 1×100
1e+1 == 10.00 == 1×101
1e+2 == 100.00 == 1×102
A normalized scientific notation expects absolute part A(*) of the number A×10b to be in the range
1 <= A < 10
Syntax
final typename CONSTANT_NAME = value;
For example,
final int DAYS_IN_NOVEMBER = 30;
final float SALES_TAX = .075F;
final double LIGHT_YEAR_MILES = 5.879e+12
Capitalize all of the letters in constants and separate words with underscores
Use meaningful names that are easy to remember
Operator Name
-------- ---------------
+ Addition
- Subtraction
* Multiplication
/ Division
% Modulus
++ Increment
-- Decrement
+ Positive sign
- Negative sign
// character arithmetic
char letter1 = 'C';
// letter1 = 'C' Unicode integer is 67
char letter2 = ++letter1;
// letter2 = 'D' Unicode integer is 68
Statements that use the same variable on both sides of the equals sign:
count = count + 1; // count is increased by 1
count = count – 1; // count is decreased by 1
total = total + 100.0; // total is increased by 100.0
total = total – 100.0; // total is decreased by 100.0
price = price * .8; // price is multiplied by .8
sum = sum + nextNumber; // sum is increased by value
// of nextNumber
Operator Name
-------- ---------------
= Plain Assignment
+= Addition
-= Subtraction
*= Multiplication
/= Division
%= Modulus
Statements that use the short-hand assignment operators to get the same results:
count += 1; // count is increased by 1
count -= 1; // count is decreased by 1
total += 100.0; // total is increased by 100.0
total -= 100.0; // total is decreased by 100.0
price *= .8; // price is multipled by .8
sum += nextNumber; // sum is increased by the value
// of nextNumber
Conditional operator (also known as arithmetic if,) is a ternary operator
Syntax:
expression1 ? expression2 : expression3
If expression1 is true, then the result of the condition is expression2.
Otherwise, the result of the condition is expression3.
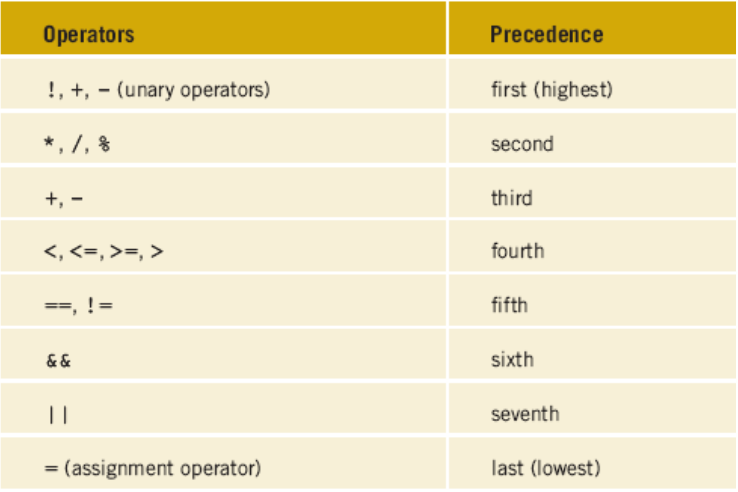
The order of precedence for arithmetic operations
Increment and decrement
Positive and negative
Multiplication, division, and remainder
Addition and subtraction

Code that calculates a discounted price using the default order of precedence:
double discountPercent = .2; // 20% discount double price = 100; // $100 price price = price * 1 - discountPercent; // price = $99.8
The above formula is incorrect, because multiplication has higher precedence than addition.
Using parentheses that specify the order of precedence remedies the problem:
price = price * (1 – discountPercent); // price = $80
Prefix and postfix increment and decrement operators behave as follows:
int a = 5;
int b = 5;
int y = ++a; // a = 6, y = 6
int z = b++; // b = 6, z = 5
Implicit casting works by converting values from less precise to more precise data types:
byte -> short -> int -> long -> float -> double
Implicit, or automatic casting is done transparently by Java.
Implicit casting converts data to the type being assigned.
Implicit casting also converts all variables in an arithmetic expression to the data type of the most precise or largest in size data type.
double grade = 93; // convert int to double
double d = 95.0;
int i = 86, j = 91;
double average = (d+i+j)/3;
// convert i and j to double values
// average = 90.666666...
Explicit casting is done by special syntax in the .java source file:
(typename) expression
An expression is preceded with a data type between the parentheses. For example,
double dGrade = 93.75
int iGrade = (int) dGrade;
int grade = (int) 93.75;
// convert double to int (grade = 93)
double d = 95.0;
int i = 86, j = 91;
double average = ((int)d+i+j)/3;
// convert d to int value (average = 90)
double result = (double) i / (double) j;
// result has decimal places
char letterChar = 65;
// convert int to char (letterChar = 'A')
char letterChar2 = (char) 65;
// this works too
int letterInt = 'A';
// convert char to int (letterInt = 65)
int letterInt2 = (int) 'A';
// this works too
import java.lang.Math;
Common static methods of the Math class
round(floatOrDouble)
pow(number, power)
sqrt(number)
max(a, b)
min(a, b)
random()
long result = Math.round(1.667); // result is 2 int result = Math.round(1.49F); // result is 1
double result = Math.pow(2, 2);
// result is 4.0 (2*2)
double result = Math.pow(2, 3);
// result is 8.0 (2*2*2)
double result = Math.pow(5, 2);
// result is 25.0 (5 squared)
int result = (int) Math.pow(5, 2);
// result is 25 (5 squared)
double result = Math.sqrt(20.25); // result is 4.5
int x = 67; int y = 23; int max = Math.max(x, y); // max is 67 int min = Math.min(x, y); // min is 23
double x = Math.random() * 100;
// result is a value >= 0.0 and < 100.0
long result = (long) x;
// converts the result from double to long
Constructors for the Integer and Double classes
Integer(int)
Double(double)
Examples creating Integer and Double objects:
Integer quantityIntegerObject = new Integer(quantity); Double priceDoubleObject = new Double(price);
NOTE: In addition to the Integer and Double classes, all other primitive data types also have corresponding wrapper classes similar to Integer and Double.
Two static methods of the Integer class
parseInt(stringName)
toString(intName)
Two static methods of the Double class
parseDouble(stringName)
toString(doubleName)
The Integer and Double toString static methods convert the corresponding primitive types to a String:
String counterString = Integer.toString(counter);
String priceString = Double.toString(price);
The opposite conversion of String objects to primitive types is also done using static methods:
int quantity = Integer.parseInt(quantityString);
double price = Double.parseDouble(priceString);
Given string str1 and str2, you can compare them by
str1.compareTo( str2 )
There can be three possible outcomes of this comparison:
A negative result if str1 < str2
A zero if the strings are equal
A positive result if str1 > str2
Java double type isn't flexible enough to provide control over how the number is rounded, and there is no way to limit the double precision in computation.
When working with currencies, double types representing dollar amounts often yield rounding errors of $0.01 or more.
For example, where an exact amount is expected, such as $5.00, the rounding error may result in $5.01. It would make development of an accounting software a nightmare, if programmers were forced to use only double type for currency.
The BigDecimal class gives program complete control over rounding behavior of foating point numbers.
Eight rounding modes are provided for the control of rounding, specified by values of the RoundingMode enumeration.
Note: this material is based on examples from online tutorial at www.opentaps.org
Currency calculations require precision of two digits after the decimal point: $5.99
Sometimes a specific type of rounding behavior is needed: tax calculations always require rounding up
Consider a bowl of ice cream that costs $10.00. If local sales tax is 0.0825 (8.25% tax rate) then the tax amount is
$10.00 * 0.0825 = $0.825 -> $0.83
where "->" represents rounding operation. The total charge to the customer becomes $10.83, and the tax collector gets $0.83 of each ice cream bowl sold.
If 1000 bowls are sold, an overpaid tax due to rounding becomes $5:
1000 * ( 0.83 - 0.825 ) = 5.0
import java.math.BigDecimal;
Constructors of the BigDecimal class:
BigDecimal(int)
BigDecimal(double)
BigDecimal(long)
BigDecimal(String)
add(value)
compareTo(value)
divide(value, scale, roundingMode)
multiply(value)
setScale(scale, roundingMode)
subtract(value)
toString()
RoundingMode enumeration specify a rounding method:
import java.math.RoundingMode;
Two of the values in the RoundingMode enumeration, such as
HALF_UP // Most commonly used rounding scheme
HALF_EVEN // "Banker's rounding" often used in the USA
For example,
subtotal.setScale( 2, RoundingMode.HALF_UP );
Rounding means discarding a fraction of the value.
The RoundingMode.HALF_UP rounding mode is the one commonly taught at school:
if the discarded fraction is >= 0.5, round up;
if the discarded fraction is < 0.5, then round down.
For example, after
BigDecimal bdRounded = bdValue.setScale(0, RoundingMode.HALF_UP);
the rounding will be
Input Rounded value
----- -------------
4.5 -> 5
1.1 -> 1
The zero parameter sets the precision scale to zero decimal points.
This rounding mode is analogous to the rounding policy used for float and double arithmetic in Java.
Same as RoundingMode.HALF_UP, except when the rounding digit is 5:
it will round down if the digit to the left of the 5 is even
it will round up if the digit to the left of the 5 is odd
For example, after
BigDecimal bdHalfEven = bdValue.setScale(0, RoundingMode.HALF_EVEN);
the rounding will be
Input Rounded value
----- -------------
2.5 -> 2 // because 2 is even, round down
7.5 -> 8 // because 7 is odd, round up
Sample program Rounding.java demonstrates differences between HALF_UP and HALF_EVEN rounding modes. A few examples of rounding differences are highlighted:
BigDecimal: 2.565
Rounded HALF_UP: 2.57
Rounded HALF_EVEN: 2.56
BigDecimal: 2.575
Rounded HALF_UP: 2.58
Rounded HALF_EVEN: 2.58
BigDecimal: 2.585
Rounded HALF_UP: 2.59
Rounded HALF_EVEN: 2.58
The import statement required for BigDecimal arithmetic is
import java.math.*; // imports all classes and
// enumerations in java.math
Sample calculation using BigDecimal:
// convert subtotal and discount percent to BigDecimal
double subtotal = 456.78;
double discountPercent = 0.2345;
final double SALES_TAX_PCT = 0.085;
BigDecimal decimalSubtotal =
new BigDecimal(Double.toString(subtotal));
decimalSubtotal =
decimalSubtotal.setScale(2, RoundingMode.HALF_UP);
BigDecimal decimalDiscountPercent =
new BigDecimal(Double.toString(discountPercent));
// calculate discount amount
BigDecimal discountAmount =
decimalSubtotal.multiply(decimalDiscountPercent);
discountAmount = discountAmount.setScale(
2, RoundingMode.HALF_UP);
// calculate total before tax, sales tax, and total
BigDecimal totalBeforeTax =
decimalSubtotal.subtract(discountAmount);
BigDecimal salesTaxPercent =
new BigDecimal(SALES_TAX_PCT);
BigDecimal salesTax =
salesTaxPercent.multiply(totalBeforeTax);
salesTax = salesTax.setScale(2, RoundingMode.HALF_UP);
BigDecimal total = totalBeforeTax.add(salesTax);
BigDecimal objects are immutable -- if you create a BigDecimal with the value of 2.00, the object will remain 2.00 and can never be changed.
The methods such as .add(), .multiply(), and so on, return a new BigDecimal object containing the result.
Therefore, the following two lines demonstrate right and wrong ways to do the math with BigDecimal:
amountA = amountA.add( amountB ); // CORRECT -- new object is created
amountA.add( amountB ); // INCORRECT -- attempting to update object "in place"
To create a BigDecimal object from another BigDecimal object, use
BigDecimal total2 = new BigDecimal(total.toString());
Notice the use of toString. When converting to/from double instead of the String, the BigDecimal often gets an unwanted (and unnecessary) high precision fractions.
For example, a double value of 1.4 becomes
double value: 1.4
BigDecimal: 1.399999999999999911182158029987476766109466552734375
Try to uncomment and use nextDouble method in the sample program Rounding.java to test this behavior.
Be careful using .equals() method to compare BigDecimals --
the .equals() compares both the values and the scale.
Instead, to compare unrounded valus of the two BigDecimals, use the .compareTo() and .signum() methods:
amountA.compareTo(amountB); // returns (-1 if A < B), (0 if A == B), (1 if A > B)
amountA.signum(); // returns (-1 if A < 0), (0 if A == 0), (1 if A > 0)
When dealing with money, it would be nice to have the amounts held by BigDecimal properly formatted.
For example, when displaying US currency you might want to include a dollar sign and a comma as a thousands separator.
The NumberFormat class, found in the java.text library, can create an appropriate object for US currency with the following code:
import java.text.NumberFormat; import java.util.Locale; BigDecimal payment = new BigDecimal("1000000.00")); NumberFormat nf = NumberFormat.getCurrencyInstance(Locale.US); double doublePayment = payment.doubleValue(); String strPayment = nf.format(doublePayment); System.out.println(strPayment);
import java.text.NumberFormat;
Three static methods of the NumberFormat class are
getCurrencyInstance()
getPercentInstance()
getNumberInstance()
Three methods of a NumberFormat object
format(anyNumberType)
setMinimumFractionDigits(int)
setMaximumFractionDigits(int)
Objects of the NumberFormat class are used for formatting real numbers (with decimal points)
The NumberFormat class has three static methods that can be used for formatting
real numbers,
currency, and
percent.
The format method returns a String for user-friendly display.
Objects of the NumberFormat class use a rounding technique called "half even" which can be used in most applications.
It is always best to format output of real numbers (BigDecimal, float or double) prior to displaying the numbers on the screen.
double price = 11.575;
NumberFormat currency = NumberFormat.getCurrencyInstance();
String priceString = currency.format(price);
// returns $11.58
double majority = .505;
NumberFormat percent = NumberFormat.getPercentInstance();
String majorityString = percent.format(majority);
// returns 50%
double miles = 15341.253;
NumberFormat number = NumberFormat.getNumberInstance();
number.setMaximumFractionDigits(1);
String milesString = number.format(miles);
// returns 15,341.3
double majority = .505;
String majorityString =
NumberFormat.getPercentInstance().format(majority);
firstName == null // equal to a null value firstName != null // not equal to a null value
The following code detects whether two strings refer to the same object in memory:
Scanner sc = new Scanner(System.in);
System.out.print("Enter string1: ");
String string1 = sc.next();
System.out.print("Enter string2: ");
String string2 = sc.next();
if (string1 == string2) // this will always be false!
System.out.println("string1 = string2");
else
System.out.println("string1 not = string2");
NOTE: Because Java stores string literals such as "Hello" in pools to reduce duplication, the equality and inequality tests for strings may not work as shown above when two String objects are assigned the same literal value.
Operator Name
-------- -----------------
&& // Logical AND
|| // Logical OR
! // Logical Not
& // Bitwise AND
| // Bitwise OR
Operators
&& // Logical AND
|| // Logical OR
are capable of short-circuiting the evaluation of the expression.
Definition: short-circuiting a process in which the computer evaluates a logical expression from left to right and stops as soon as the value of the expression is known.
switch (switchExpression)
{
case label1:
statements
break;
[case label2:
statements
break;] ...
[default:
statements
break;]
}
In Java, switch, case, break, and default are reserved words
The switchExpression (also called the selector) can of types
int, byte, short, char
enumerated types
String
Character, Byte, Short, or Integer object
In a switch statement, the switchExpression is evaluated first to determine which action statements should be selected for execution
The statements that follow the matching case value are executed
A particular case value must appear only once in the switch statement
One or more statements may follow a case label -- no need to use braces to turn multiple statements into a single compound statement
The default label is optional
switch (grade) {
case 'A':
System.out.println("The grade is A.");
break;
case 'B':
System.out.println("The grade is B.");
break;
case 'C':
System.out.println("The grade is C.");
break;
case 'D':
System.out.println("The grade is D.");
break;
case 'F':
System.out.println("The grade is F.");
break;
default:
System.out.println("The grade is invalid.");
}
switch (productID) {
case 1:
productDescription = "Hammer";
break;
case 2:
productDescription = "Box of Nails";
break;
default:
productDescription = "Product not found";
break;
}
switch (productCode) {
case "hm01":
productDescription = "Hammer";
break;
case "bn03":
productDescription = "Box of Nails";
break;
default:
productDescription = "Product not found";
break;
}
A switch statement that falls through case labels
switch (dayOfWeek)
{
case 2:
case 3:
case 4:
case 5:
case 6:
day = "weekday";
break;
case 1:
case 7:
day = "weekend";
break;
}
do {
statements
} while (booleanExpression);
for ( initExpr; booleanExpr; incrementExpr ) {
statements
}
The following code fragment stores the numbers 0 through 4 in a string object:
String numbers = "";
for ( int num = 0; num < 5; ++num ) {
numbers += num;
numbers += " ";
}
The syntax of the break statement:
break;
A break statement that exits the inner loop:
for (int i = 1; i < 4; i++) {
System.out.println("Outer " + i);
while ( true ) {
int number = (int) (Math.random() * 10);
System.out.println(" Inner " + number);
if (number > 7)
break;
}
}
break labelName;
The structure of the labeled break statement
labelName:
loop declaration
{
statements
another loop declaration
{
statements
if (conditionalExpression)
{
statements
break labelName;
}
}
}
outerLoop:
for (int i = 1; i < 4; i++)
{
System.out.println("Outer " + i);
while (true)
{
int number = (int) (Math.random() * 10);
System.out.println(" Inner " + number);
if (number > 7)
break outerLoop;
}
}
The syntax of the continue statement is:
continue;
A continue statement jumps to the beginning of the loop:
for (int j = 1; j < 10; j++) {
int number = (int) (Math.random() * 10);
System.out.println(number);
if (number <= 7)
continue;
System.out.println("This number is greater than 7");
}
The syntax of the labeled continue statement
continue labelName;
The structure of the labeled continue statement
labelName:
loop declaration
{
statements
another loop declaration
{
statements
if (conditionalExpression)
{
statements
continue labelName;
}
}
}
A labeled continue statement jumps to the beginning of the outer loop:
outerLoop:
for (int i = 2; i < 20; i++) {
for (int j = 2; j < i-1; j++)
{
int remainder = i % j;
if (remainder == 0)
continue outerLoop;
}
System.out.println(i);
}
The basic syntax for coding a static method
public|private static returnType methodName([parameterList])
{
statements
}
A static method with no parameters and no return type
private static void printWelcomeMessage()
{
System.out.println("Hello New User");
}
Calling static method in the same class
methodName([argumentList])
A call statement with no arguments
printWelcomeMessage();
A call statement that passes two arguments
double grade = calculateGrade( maxPoints, studentScore );