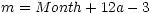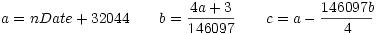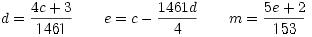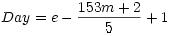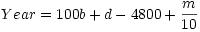Course List: http://www.c-jump.com/bcc/

Assignment a4: Serial Julian Date (Part 1)

1. Assignment Description
2. User interface
3. Getting started
4. Back to Gregorian calendar
5. Programming requirements
6. How to Submit

1. Assignment Description

• In this assignment you will write a program that uses dates of Gregorian calendar, which is the calendar commonly used today. In doing so, you will have a chance to create a number of useful C++ functions to convert Gregorian date to a serial Julian date, which is simply an integer that stores the number of days since November 24 4714 BC, otherwise known as the Julian Period (this is January 1st 4713 BC in the Julian Calendar.)

• You will also explore the functionality of C++ streams while prompting, validating, and processing user input of various dates. One week is the time frame to complete your work. Start early, since you may discover things looking trivial at the beginning appear to take longer time to implement than you originally expected.

   

2. User interface

• Input three integer variables from the user, corresponding to the month, day, and year. Don't worry about any input validation at this stage of your project.

  The program converts this date to serial Julian date and prints the result. For example,

  
   Enter a date in MM DD YYYY format (separated by spaces): 7 4 1776
                                     Serial Julian date is: 2369916
  
  

  (User input is highlighted.)

• Repeat the above steps in an endless loop. Exit the program if the user enters zero for the month, day, and year.

   

3. Getting started

1. Please note: the type of all variables in this project is int.

2. Use function

   
       int serial_julian_date( int Month, int Day, int Year );
   
   

   to calculate and return the serial Julian date nDate as follows:

   
   
   
   
   
   
   
   
   

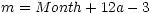
3. All divisions in these formulas are integer divisions. The solution perfectly accounts for all leap years and varying month lengths to produce a unique serial number for each and every day. The limitation is only the numerical capacity of the integer data type on your machine.

4. You must pay some special attention to the operator precedence when translating the above equations to the C++ expressions. Use parentheses were appropriate, and if in doubt about the order of calculation.

5. Test your program with a few dates. You should be able to obtain the following serial dates:

   
         7/4/1776   2369916
       12/31/2000   2451910
         2/8/2007   2454140
         2/9/2007   2454141
   
   

6. Your program should implement an endless loop, asking user for input and printing the calculated serial date on the screen, then repeat.

    

4. Back to Gregorian calendar

1. Add three more functions to your program,

   
       int serial_2_month( int nDate );
       int serial_2_day( int nDate );
       int serial_2_year( int nDate );
   
   

   where nDate is the value calculated by the serial_julian_date() function from above. The new functions should return calendar month, day, and year, respectively.

2. Performing the inverse calculations for the Gregorian calendar are achieved using the following formulas:

   
   
   
   
   
   
   
   
   

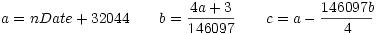
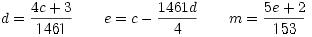
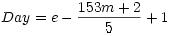
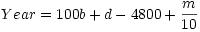
   Here, a, b, c, d, e, and m are temporary local variables. Month, Day, and Year are the results that you have to return from your functions.

3. Again, the operator precedence and order of evaluation of the expressions are paramount in those calculations. Since we have to deal with integer division,

   
       int Month = m + 3 - 12 * ( m / 10 ); // CORRECT
   
   

   and

   
       int Month = m + 3 - ( 12 * m ) / 10; // *** WRONG!
   
   

   give different results, of which the last version is incorrect due to misplaced parentheses.

4. Add calls to new functions to your main loop and display the results on the screen. Visually inspect and verify that inverse calculations return expected results.

   
       Enter a date in MM DD YYYY format (digits separated by spaces): 7 4 1776
                                                Serial Julian date is: 2369916
                                               Back to Gregorian date: 7 4 1776
   
   

5. To learn more about calendars, visit The Calendar FAQ

    

5. Programming requirements

• Each C++ function must have comments explaining in substantial detail what it does and why. Not following this requirement will result in a deduction of 10 pts per each undocumented function.

   

6. How to Submit

• You should submit all source files (.cpp) and header files (.h) from your project. It may be helpful to ZIP your src subdirectory and upload everything in a single ZIP file.

• Select Weekly Assignments -> Assignment a4 and upload your source code.