Arithmetic Operations and Logical Functions

A key requirement of digital computers is the ability to use logical functions to perform arithmetic operations.
If we can add two binary numbers, then we should be able to:
- subtract them, and
- perform multiplication and division.

These four possibilities, and the resulting sums, are:

Therefore, we can transform our results into a truth table, shown on the right.
Suddenly, this looks familiar:
- The carry output is a simple AND function.
- The sum is an XOR.

Corresponding logic gate circuit, which adds inputs A and B, is known as half adder.

A half adder circuit has one significant drawback:
- since pair of bits can produce an output carry,
- in addition to the inputs A and B, we need to account for a possible carry over from a bit of the lower order of magnitude.
- Unfortunately, half adder has no support for such carry over input by design.
Therefore, the combination requires not two, but three inputs to make the adder circuit more useful.
The circuit that does the entire job is called a full adder.

To construct a full binary adder circuit, we need three inputs and two outputs, as specified by the following truth table:

To implement the adder logic, we could combine two half-adder circuits together:
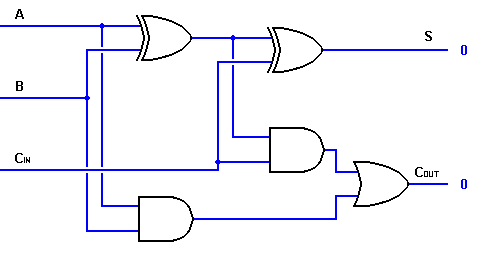
For the reasons explained later, we will examine a different version of the full adder circuit, as well as its functional details.
The second version of the full adder will have more primitive, brute force^(*) implementation.
_____________
^(*) Hacker Slang

The new circuit combines three inputs: two input bits and a carry.
The gate-level description of a full adder follows:
Combination of AND-gates is a decoder circuit for each possible combination of inputs.
Decoder produces output of a single 1 (with the rest of 0s) for each unique combinaton of input signals.
The OR gates re-combine unique output 1 into desired combination of carry and sum outputs.
Note that AND-gate on top of the circuit is not connected to either of the OR-gates, because it should never produce any 1s in either output.

A circuit for adding two 4-bit binary numbers:

So far we explored a one-bit full adder.
To add multiple binary bits together, we must include a possible carry over from the lower order of magnitude, and send it as an input carry to the next higher order of magnitude bit.
Multibit addition requires full adders with carry lines to be cascaded (chained together.)
See also: binary subtraction article.

One-bit full adder logic demonstrates a programmable logic array, or PLA, which is a collection of logic functions between:
- unique input pattern, presorted by AND-gate array (decoder) on the left side, and
- OR-gate array one the right side.
AND array corresponds to the number of rows in the truth table.

For n rows we need 2ⁿ input AND-gates to construct the circuit.
For example, one-bit full adder had 3 inputs and required 8 = 2³ input AND gates.

The number of OR-gates corresponds to the number of output columns in the truth table.
PLA implementation is very simple: connect AND-gate output to the input of OR-gate as follows:
- If row of the corresponding AND-gate requires output 1, make a connection.
- If the truth table raw requires output 0, do not make a connection.

This kind of approach to implement the truth table implies the notion of being programmable.
We program our connections between the AND- and OR-gates while implementing desired logic functions.
Note that besides AND and OR the PLA may also include inverters.

We say that a set of gates
- {AND, OR, NOT}
is logically complete, if we are able to:
1. draw a set of programmable connections between gates without any other kind of gate, and
2. completely satisfy the requirements of the truth table.
We may also say that such set of gates {AND, OR, NOT}
- is sufficient to build an implementation of a given truth table, and
- we don't need any other gates to do the job.